Les clinomètres
Des instruments du 19e siècle aux usages variés
5e à 11e année (Ontario)
3e cycle du primaire au 2e cycle du secondaire (Québec)
Les premiers arpenteurs, explorateurs et scientifiques se sont servis de clinomètres pour évaluer rapidement l’inclinaison et la hauteur des objets qu’ils voyaient. Bien que ces instruments ne soient plus courants, ils demeurent utiles. Découvrez comment utiliser un clinomètre pour déterminer la hauteur d’un objet du quotidien.
Au moyen de fichiers 3D téléchargeables et de fiches d’activité, les élèves étudient les clinomètres, instruments du 19e siècles. Les activités mettent l’accent sur l’utilisation d’un clinomètre pour déterminer la hauteur d’un objet et la latitude du lieu où vous vous trouvez.
Vous pouvez reproduire les fiches d’activité et les fichiers d’impression 3D du module pour votre classe, au besoin.

Partager :
Liens avec le curriculum
Grâce à cette activité, vos élèves :
- Découvriront les clinomètres et une façon simple de les utiliser pour déterminer la hauteur.
- Utilise les principes de la trigonométrie (en particulier la fonction tangente) pour estimer la hauteur d’un objet.
- Apprendre à déterminer l’altitude solaire (l’angle du Soleil au-dessus de l’horizon) à l’aide d’un clinomètre. Les élèves seront ensuite en mesure d’utiliser cette valeur pour déterminer approximativement la latitude à laquelle ils se trouvent.
5e année
Mathématiques (géométrie et sens de l’espace)
7e année
Mathématiques (géométrie et sens de l’espace)
10e année
Mathématiques : académiques et appliquées (trigonométrie)
11e année
Géographie (introduction aux technologies spatiales)
3e cycle du primaire au 2e cycle du secondaire
Les clinomètres et la hauteur (méthode simple)
Au cours de cette activité, les élèves et vous fabriquerez un clinomètre et apprendrez à vous en servir pour déterminer la hauteur d’un objet. Il en existe une version fondée sur une méthode simple, ainsi qu’une version fondée sur une méthode avancée, qui repose sur des principes de trigonométrie.
Matériel
- Clinomètre imprimé en 3D
- Rapporteur d’angles imprimé
- Bâton de colle
- Ruban à mesurer
Instructions
Fabrication du clinomètre
- Les termes énoncés dans l’image de droite seront employés dans les instructions.

- Au moyen du bâton de colle, fixez le rapporteur d’angles sur le corps du clinomètre. Il faut placer le rapporteur d’angles de sorte que la ligne du « 0 » arrive à égalité avec le rebord et que la pointe soit vis à vis du trou (voir l’illustration à gauche), ce qui assurera l’exactitude des mesures.

- Insérez le bras du clinomètre dans le trou situé sur le corps de l’instrument. Placez d’abord l’extrémité la plus courte. Si le bras ne bouge pas librement après son insertion, c’est peut-être parce que vous avez inséré le mauvais côté.

Remarque : Si vous ne souhaitez pas utiliser le bras (ou s’il se brise), vous pouvez nouer un fil sur le corps du clinomètre (là où est situé le trou) et attacher une pesée (un trombone ou une rondelle, p. ex.) à l’autre extrémité du fil.
- Lorsque le clinomètre est incliné, le bras indique un nombre sur le rapporteur d’angles. Ce nombre représente l’angle d’inclinaison du clinomètre par rapport à l’horizon. Faites l’essai du clinomètre. Le principal point à retenir, c’est que le bras doit glisser librement sur la surface du corps de l’instrument.

Mesure de la hauteur d’un objet
Remarque : Il est préférable de faire cette activité à deux.
- Choisissez un objet situé à proximité dont vous souhaitez mesurer la hauteur et faites-y face.
- Regardez dans le clinomètre et inclinez-le doucement jusqu’à ce qu’il atteigne un angle de 45 degrés.
- Dirigez-vous vers l’objet tout en maintenant le clinomètre à un angle de 45 degrés. C’est alors que le deuxième membre du groupe peut jouer un rôle en s’assurant que rien ne vous fasse trébucher.
- Cessez de marcher lorsque vous voyez le sommet de l’objet dans le centre de l’oculaire du clinomètre.
- Mesurez la distance qui vous sépare de l’objet (d dans l’illustration ci-dessus). Il s’agit également la hauteur de l’objet à partir du niveau du clinomètre (h2). Pourquoi en est-il ainsi?
- La hauteur que vous avez mesurée n’est pas la hauteur réelle de l’objet. Pour obtenir cette dernière, il faut ajouter la distance à partir du sol jusqu’au niveau où se trouvait le clinomètre lorsque vous avez pris la mesure (h2 dans l’illustration ci-dessous).


Explications scientifiques
Le fonctionnement du clinomètre repose sur des principes de trigonométrie. Dans cette activité, la personne portant le clinomètre le tient à un angle de 45 degrés et se dirige vers l’objet jusqu’à ce qu’elle en voie le sommet. Nous allons supposer que cet objet est un arbre. À ce point, il y a formation d’un triangle dont un des angles est de 90 degrés, et les deux autres, de 45 degrés. C’est un triangle isocèle. Les deux côtés qui se joignent à 90 degrés sont de longueur égale (voir l’illustration ci-dessous). Ils correspondent à la distance entre le clinomètre et l’arbre (d), et à la hauteur entre le niveau du clinomètre et le sommet de l’arbre (h1). Dans cette activité, c’est en déterminant d qu’on peut connaître h1.
Comme indiqué dans les instructions, h1 n’est pas la hauteur réelle de l’arbre : c’est la distance entre le niveau du clinomètre au moment de la mesure et le sommet de l’arbre. Pour obtenir la hauteur réelle de l’arbre, il faut ajouter h2, c’est à dire la distance entre le sol et le niveau du clinomètre (voir l’illustration ci-dessus).
La collection d’Ingenium comprend plus de 150 000 objets, dont un grand nombre ont trait aux clinomètres.
Les clinomètres et la hauteur (méthode avancée)
Les premiers arpenteurs, explorateurs et scientifiques se sont servis de clinomètres pour évaluer rapidement l’inclinaison et la hauteur des objets qu’ils voyaient. Bien que ces instruments ne soient plus courants, ils demeurent utiles. Découvrez comment utiliser un clinomètre pour déterminer la hauteur d’un objet du quotidien.

Matériel
- Clinomètre imprimé en 3D
- Rapporteur d’angles imprimé
- Bâton de colle
- Calculatrice
- Ruban à mesurer
Instructions
Fabrication du clinomètre
- Suivez les instructions de la section “Les clinomètres et la hauteur (méthode simple)»
Mesure de la hauteur d’un objet
- Choisissez un objet situé à proximité dont vous souhaitez mesurer la hauteur et tenez-vous à une certaine distance de cet objet.
- Regardez dans le clinomètre de sorte que le sommet de l’objet dont vous souhaitez mesurer la hauteur se trouve au centre de l’oculaire.
- Prenez note de l’angle indiqué par le bras du clinomètre (A dans l’image ci-dessus). Si vous avez de la difficulté à le lire, appuyez le bras sur le rapporteur d’angles lorsqu’il a cessé de bouger.
- Mesurez la distance qui vous sépare de l’objet (d dans l’image ci-dessus).
- Déterminer la hauteur de l’objet au-dessus du niveau du clinomètre (h1 dans l’image ci-dessus) au moyen de l’équation suivante : hauteur (h1) = distance (d) x tangente (angle A)
- Pouvez-vous expliquer pourquoi cette équation fonctionne?La hauteur que vous avez mesurée n’est pas la hauteur réelle de l’objet. Pour obtenir cette dernière, il faut ajouter la distance à partir du sol jusqu’au niveau où se trouvait le clinomètre lorsque vous avez pris la mesure (h2 dans l’image).

Suggestion
Le clinomètre dont on a tiré un modèle 3D a d’abord servi à mesurer la hauteur de la base des nuages, ce que vous pouvez aussi essayer. Tout ce qu’il vous faut de plus pour le faire est un appareil d’éclairage très puissant (comme un spot portatif) et l’aide d’une deuxième personne.
À la nuit tombée, demandez à la deuxième personne de se tenir sous des nuages et de diriger la lumière droit vers le ciel. Vous devriez voir un point lumineux là où la lumière touche au bas du nuage. Suivez les instructions qui précèdent pour déterminer la hauteur de ce point lumineux. Étant donné la hauteur des nuages, vous devrez probablement vous tenir à environ 100 m de la deuxième personne.

Explications scientifiques
Le fonctionnement du clinomètre repose sur des principes de trigonométrie. Lorsqu’on mesure la hauteur d’un objet (un arbre, p. ex.), la distance entre le clinomètre et cet objet (d), la hauteur de l’arbre à partir de celle du clinomètre (h1) et la diagonale entre le sommet de l’arbre et le clinomètre forment un triangle (voir l’illustration ci-dessous).
Dans un triangle rectangle, la tangente de l’un des angles qui ne sont pas de 90 degrés est égale au rapport de la longueur du côté opposé à l’angle sur la longueur du côté adjacent à l’angle :
tan (angle) = longueur du côté opposé ÷ longueur du côté adjacent
En substituant les lettres employées dans le diagramme ci-dessus, nous obtenons :
tan (angle A) = h1 ÷ d
Dans un triangle rectangle, la tangente de l’un des angles qui ne sont pas de 90 degrés est égale au rapport de la longueur du côté opposé à l’angle sur la longueur du côté adjacent à l’angle :
tan (angle) = longueur du côté opposé ÷ longueur du côté adjacent
En substituant les lettres employées dans le diagramme ci-dessus, nous obtenons :
tan (angle A) = h1 ÷ d
Ce qui donne :
h1 = d x tan (angle A)
Nous pouvons mesurer d. Le clinomètre mesure l’angle A. Ces deux variables étant connues, la valeur de h1 peut être calculée.
Comme indiqué dans les instructions, h1 n’est pas la hauteur réelle de l’objet : c’est la distance entre le niveau du clinomètre au moment de la mesure et le sommet de l’objet. Pour obtenir la hauteur réelle de l’objet, il faut ajouter h2, c’est à dire la distance entre le sol et le niveau du clinomètre.
La collection d’Ingenium comprend plus de 150 000 objets, dont un grand nombre ont trait aux clinomètres.
Clinomètres – déterminer sa position
Il est possible de déterminer sa position grâce à de nombreuses technologies modernes. Mais comment peut-on le faire sans celles-ci? En se servant du soleil. Découvrez-le en réalisant cette activité.
Matériel
- Clinomètre imprimé en 3D
- Rapporteur d’angles imprimé
- Bâton de colle
- Calculatrice
- Ruban à mesurer (facultatif)
Fabrication du clinomètre
- Suivez les instructions de la section Les clinomètres et la hauteur (méthode simple)
Détermination de la latitude
Vous pouvez utiliser la hauteur du soleil (l’angle du soleil au-dessus de l’horizon) pour déterminer la latitude de l’endroit où les élèves et vous vous trouvez.
Calcul de la hauteur du soleil
Deux méthodes possibles de détermination de la hauteur du soleil sont décrites ci-dessous. La première est plus directe, mais plus difficile.
Remarque : Peu importe la méthode utilisée, il faut s’assurer de ne pas regarder directement le soleil, ce qui risque de causer des lésions oculaires.
La hauteur du soleil 1 : méthode directe
- Tenez le clinomètre en face de vous de manière à voir son ombre au sol. Cette ombre devrait être totalement noire. Pour l’illustrer, nous avons inclus une photo de l’ombre d’un clinomètre sur un morceau de plastique blanc (voir l’image à droite).


- Inclinez le clinomètre de sorte que sa partie avant pointe directement vers le soleil, ce qui peut être un peu difficile. Lorsque vous aurez réussi, vous verrez un petit cercle de lumière au sol, au milieu de l’ombre du clinomètre (voir l’image ci-dessus, à droite).
- Lisez l’angle indiqué par le clinomètre. Il s’agit de la hauteur du soleil.
La hauteur du soleil 2 : méthode indirecte
- Trouvez un objet dressé relativement droit qui projette une ombre (comme un arbre).
- Mesurez la longueur de l’ombre.
- Déterminez la hauteur de l’objet au moyen de la méthode (simple ou avancée) utilisée dans l’une des activités « Les clinomètres et la hauteur », dont vous trouverez la description sur le même site Web ou vous avez obtenu cette activité.
Remarque : Pour effectuer cette mesure, il est important de ne pas se tenir au sommet de l’ombre de l’objet. Si vous le faites, vous allez probablement regarder le soleil directement. - Utilisez l’équation ci-dessous pour déterminer la hauteur du soleil :Hauteur du soleil = tan-1 (hauteur de l’objet ÷ longueur de l’ombre)
Suggestion
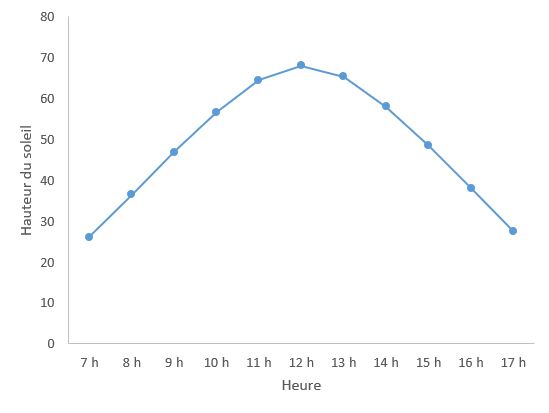
Demandez aux élèves de déterminer la hauteur du soleil tout au long de la journée. Si vous tracez un graphique de vos résultats (les variables étant l’heure et la hauteur du soleil), vous constaterez que la position du soleil change. Un tel graphique est illustré ci-dessous.
Suggestion
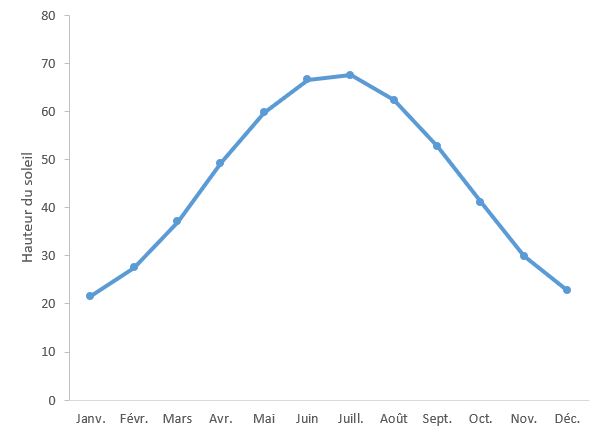
Demandez aux élèves de déterminer la hauteur du soleil à midi tous les jours (ou toutes les semaines ou tous les mois) pendant une certaine période. Les valeurs obtenues montreront l’incidence de la trajectoire orbitale de la Terre autour du soleil. Voici un exemple du graphique obtenu pour le premier jour de chaque mois à Ottawa, au Canada.
Calcul de la latitude
Calculez votre latitude au moyen de l’équation suivante :
Latitude = 90 – hauteur du soleil +/- déclinaison
Remarque : Une valeur positive indique une latitude dans l’hémisphère nord, tandis qu’une valeur négative indique une latitude dans l’hémisphère sud.
La déclinaison (c’est à dire la déclinaison solaire) est l’angle que fait le soleil avec le plan formé par l’équateur (voir l’illustration à droite).
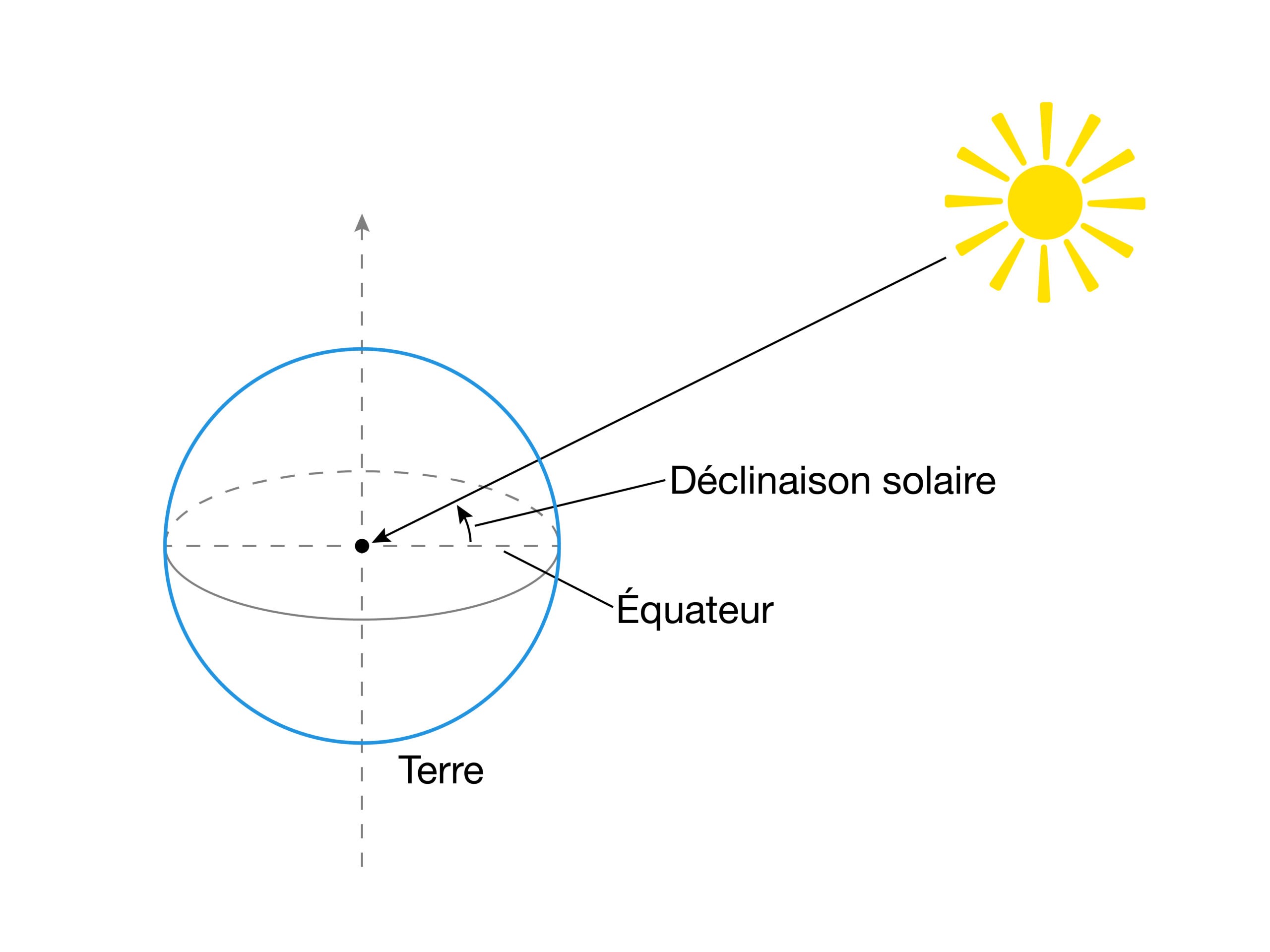
La déclinaison dépend de l’inclinaison de la Terre et de sa rotation autour du soleil. Elle est positive lorsque le soleil est au nord de l’équateur, et négative lorsqu’il est au sud de l’équateur. Pour évaluer la déclinaison un jour donné, vous pouvez utiliser l’équation suivante :
Déclinaison (en degrés) = -23,45 x cos (360 ÷ 365 x (NJA + 10))
La valeur NJA est le numéro du jour de l’année. Par exemple, celle du 1er janvier est 1; celle du 15 janvier est 15; celle du 1er février est 32 (puisque janvier compte 31 jours, auxquels il faut ajouter 1 jour). Vous trouverez un calendrier indiquant les NJA ici (site web en anglais).
L’addition ou la soustraction de la déclinaison dépend de la période de l’année et de l’endroit où vous vous trouvez sur la Terre. Si vous êtes dans l’hémisphère nord et que le soleil se trouve au sud de vous à midi, il faut additionner la déclinaison (c’est toujours le cas au Canada).
Remarque : Lorsque la déclinaison est négative, il faut la soustraire (c’est à dire ajouter un nombre négatif). En revanche, si vous vous trouvez dans l’hémisphère sud et que le soleil est au nord de vous, il faut soustraire la déclinaison.
Si vous vous trouvez dans l’hémisphère nord et que le soleil est au nord de vous (ce qui ne peut arriver que si vous êtes à une faible latitude en été), il faudra soustraire la déclinaison. Toutefois, la latitude résultante sera négative. Vous devrez donc utiliser sa valeur absolue (c’est à dire la rendre positive).
De même, si vous vous trouvez dans l’hémisphère sud et que le soleil est au sud de vous, il faudra additionner la déclinaison, puis utiliser la valeur absolue de la latitude résultante.
Exemple de calcul de la latitude :
Lieu : Ottawa, Canada
Date et heure : 1er juin 2018, midi
Latitude = 90 – hauteur du soleil +/- déclinaison
a) Hauteur du soleil mesurée = 67 degrés
b) Déclinaison = -23,45 x cos (360 ÷ 365 x (NJA + 10))
Pour le 1er juin 2018, la valeur NJA est 152.
Déclinaison = -23,45 x cos (360 ÷ 365 x (152 + 10))
= -23,45 x cos (159,78)
= 22
c) Latitude = 90 – hauteur du soleil +/- déclinaison
Étant donné que nous sommes au Canada, nous devons ajouter la déclinaison.
Latitude = 90 – hauteur du soleil + déclinaison
= 90 – 67 + 22
= 45
Étant donné que la valeur est positive, notre calcul donne 45˚ N pour Ottawa, Canada, ce qui est la valeur exacte.
Explications scientifiques
Variation de la hauteur du soleil pendant la journée
C’est à la rotation de la Terre que nous devons le jour et la nuit. Lorsque la Terre tourne, un côté de la planète est de plus en plus exposé au soleil, qui semble monter dans le ciel. À midi, ce côté de la planète commence à s’éloigner du soleil, ce qui diminue son exposition et donne l’impression que le soleil descend.
Variation de la hauteur du soleil pendant l’année
Chaque année, la Terre parcourt une orbite autour du soleil. Lorsqu’on crée un plan de cette orbite, on constate que l’axe de la Terre ne lui est pas perpendiculaire. En fait, il est incliné à un angle de 23,5 degrés par rapport à la verticale.
C’est à cette inclinaison et à l’orbite que décrit la Terre autour du soleil que l’on doit les saisons. Ce sont aussi les raisons pour lesquelles la hauteur du soleil à midi (ou à tout autre moment de la journée) varie tout au long de l’année. En été, l’hémisphère nord est incliné vers le soleil; en hiver, il est incliné dans la direction opposée. C’est pourquoi le soleil y est plus haut dans le ciel en été.

La collection d’Ingenium comprend plus de 150 000 objets, dont un grand nombre ont trait aux clinomètres.
Artéfact : Clinomètre
Aussi appelé inclinomètre (ou, dans le domaine de l’arpentage, niveau d’Abney), le clinomètre sert à mesurer les angles. Il s’apparente à des instruments comme le sextant et l’astrolabe, qui ont principalement été utilisés par les navigateurs pour mesurer les angles entre les étoiles (en particulier l’étoile Polaire) et l’horizon.
Le clinomètre, lui, sert principalement à mesurer des angles sur terre. Les renseignements obtenus peuvent être utilisés pour déterminer, par exemple, la pente d’une côte ou la hauteur d’une montagne, d’un arbre ou d’un nuage. Le clinomètre existe depuis très longtemps. Au début, il s’agissait d’un simple fil à plomb. Vers la fin du 18e siècle, il était devenu un instrument complexe, qui se composait notamment de niveaux à bulle, de mires et de télescopes. Le niveau d’Abney est un clinomètre bien connu. Inventé par William Abney avant 1880, il était constitué d’un petit télescope, d’un demi-cercle gradué et d’un tube à bulle.
Précisions sur l’artéfact
- Clinomètre, vers 1951
- Fabricant : Ministère des Transports, Division de la météorologie (Canada)
- No d’artéfact : 1987.0738.001
Le clinomètre illustré à droite a été conçu et utilisé par le Service météorologique du Canada pour déterminer l’altitude de la base des nuages du début des années 1950 jusqu’en 1958. Fait de pièces en fonte et en laiton, il était peint en noir.
Fait intéressant
Dans une lettre de 1831 adressée à John Henslow, Charles Darwin se montrait enthousiaste au sujet de son nouveau clinomètre et de l’utilisation qu’il allait en faire au cours de ses excursions géologiques.
Fichiers à télécharger
Fichiers d’impression 3D
Téléchargez et imprimez votre propre clinomètre. Utilisez ces fichiers .stl au cours des activités décrites ci-dessus.
- Fichiers d’impression 3D (ZIP, 750 Ko)
Modèles
- Rapporteur angles imprimé (PDF, 44 Ko)
À découvrir
Modèle anatomique
Découvrez l’incroyable corps humain et la manière dont des organes complexes remplissent toutes sortes de fonctions qui travaillent ensemble pour nous maintenir en vie, grâce à une série de mini-activités et de démonstrations amusantes et éducatives proposées par Ingenium.

Artefacts associés au beurre
Fabriquez votre propre beurre dans votre classe grâce à ces fichiers et activités imprimables en 3D. Créez ensuite un étampe pour décorer et nommer votre beurre à l’aide d’un étampe à beurre comme celle utilisée aux 18e et 20e siècles.

Zootrope
Explorez le zootrope, un dispositif d’animation précoce qui utilise un tour d’optique pour produire des images en mouvement. Ce plan de cours contient des instructions sur la façon de construire votre propre zootrope imprimé en 3D, de l’assembler et de le faire fonctionner. Les élèves seront captivés par la science qui se cache derrière cet artefact de la collection Ingenium.